A random experiment is a procedure that can be repeated an infinite number of times and has a set of possible outcomes. The sample space S of a certain random experiment is the totality of all its possible outcomes.
Example: ``Randomly pick a card from a deck of 10 cards labeled
![]() '' is a random experiment. The sample space is a set of
the 10 possible outcomes:
'' is a random experiment. The sample space is a set of
the 10 possible outcomes:
![]() .
.
An random event ![]() is a subset of
is a subset of ![]() ,
, ![]() .
. ![]() can be a null
set
can be a null
set ![]() (empty set), proper subset (e.g., a single outcome), or the
entire
(empty set), proper subset (e.g., a single outcome), or the
entire ![]() . Event
. Event ![]() occurs if the outcome
occurs if the outcome ![]() is a member of
is a member of ![]() ,
, ![]() .
The probability of an event
.
The probability of an event ![]() ,
, ![]() , is a real-valued function that maps
, is a real-valued function that maps
![]() to a real number
to a real number
![]() . In particular,
. In particular,
![]() ,
and
,
and ![]() .
.
Example: ``The randomly chosen card has a number smaller than 4'' is
a random event, which is represented by a subset
![]() .
The probability of this event
.
The probability of this event ![]() is
is ![]() . Event
. Event ![]() occurs if the
outcome is one of the member of
occurs if the
outcome is one of the member of ![]() (e.g., 2).
(e.g., 2).
The triple of sample space, events and probability is called the probability space.
The conditional probability ![]() is the probability that event
is the probability that event ![]() will occur given that event
will occur given that event ![]() has already occurred. If event
has already occurred. If event ![]() is
independent of event
is
independent of event ![]() , then
, then ![]() .
.
Let ![]() and
and ![]() be two events defined over
be two events defined over ![]() .
.
- The Intersection of A and B is an event whose outcomes
belong to both
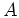 and
and 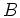 ,
, 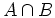 .
.
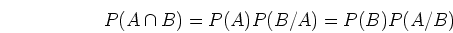
If A and B are independent, i.e.,
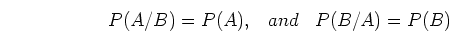
then
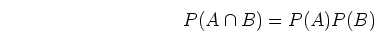
- The Union of A and B is an event whose outcomes belong to
either
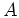 or
or 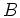 ,
, 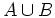 .
.
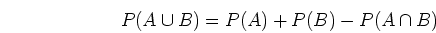
If A and B are mutually exclusive, i.e.,

then
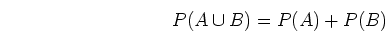
Let
![]() be a set of
be a set of ![]() events that partition the
sample space
events that partition the
sample space ![]() in such a way that
in such a way that

and
then for any event
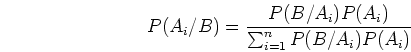
Proof
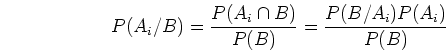
but
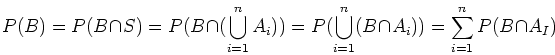
Substituting this expression of
A random variable ![]() is a real-valued function whose domain is the sample
space
is a real-valued function whose domain is the sample
space ![]() . In other words, this function maps every outcome
. In other words, this function maps every outcome ![]() into a
real number
into a
real number ![]() . Random variables
. Random variables ![]() can be either continuous or discrete.
can be either continuous or discrete.
The cumulative distribution function of a random variable X is defined
as
and we have
The density function ![]() of a random variable
of a random variable ![]() is defined by
is defined by
i.e.,
and we have
and
If a random variable ![]() can only take one of a set of finite number of
discrete values
can only take one of a set of finite number of
discrete values
![]() , then its probability
distribution is
, then its probability
distribution is
and we have
and

The cumulative distribution function is
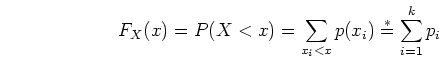
where the last equation assumes
The expectation or mean value of a random variable ![]() is defined
as
is defined
as
if
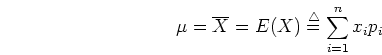
if
The variance of a random variable ![]() is defined as
is defined as
if
![\begin{displaymath}\sigma^2=Var(X)\stackrel{\triangle}{=}E[(X-\mu)^2]
=\sum_{i=1}^n (x_i-\mu)^2 p_i \end{displaymath}](img56.png)
if
The standard deviation of ![]() is defined as
is defined as
We have
Random variable ![]() has a normal distribution if its density function is
has a normal distribution if its density function is
It can be shown that
and
A function ![]() of a random variable
of a random variable ![]() is also a random variable. If the
density function of
is also a random variable. If the
density function of ![]() is
is ![]() , the density function of
, the density function of ![]() can be
found as shown below.
can be
found as shown below.
Consider the cumulative distribution function of ![]() :
:
where
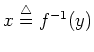 can be considered as a dummy
variable. Then we can obtain the density function of
can be considered as a dummy
variable. Then we can obtain the density function of ![\begin{displaymath}p_Y(y)=\frac{d}{dy}F_Y(y)=
\frac{d}{dy}\int_{-\infty}^x p_X(\xi)d\xi=
\left[ p_X(x)\frac{dx}{dy}\right]_{x=f^{-1}(y)} \end{displaymath}](img72.png)
The equation marked by * is based on the assumption that
and
![\begin{displaymath}p_Y(y)=\frac{d}{dy}F_Y(y)=
\frac{d}{dy}\int_x^{\infty} p_X(\xi)d\xi=
\left[ -p_X(x)\frac{dx}{dy}\right]_{x=f^{-1}(y)} \end{displaymath}](img76.png)
Considering both cases, if
![\begin{displaymath}p_Y(y)=\left[\; p_X(x) \left\vert \frac{dx}{dy} \right\vert \;\right]_{x=f^{-1}(y)}
\end{displaymath}](img77.png)