The basic idea

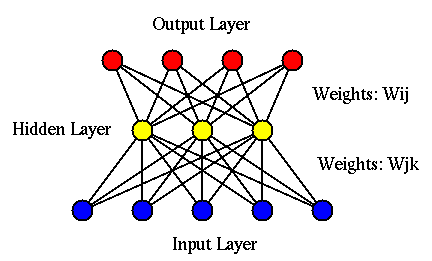
Similar to the perceptron network, back propagation network (BPN) is also a typical supervised learning network. But different from perceptron network, BPN is composed of three layers of nodes: the input, hidden, and output layers with $N$, $L$, and $M$ nodes, respectively. Each node is fully connected to all nodes in the previous layer.

Due to the two levels of learning, BPN is much more powerful than the perceptron network in the sense that it can handle nonlinear classification problems.

The two-phase classification process is:

• Training: The training data are a set of pattern pairs $\{({\bf x}_p, {\bf y}_p), p=1,2,...,K\}$, where ${\bf x}_p$'s are the input patterns and ${\bf y}_p$'s are the desired output patterns -- the correct responses.

  In training phase the following two steps are repeated for all input patterns presented to the input layer in random order:

  • Present an input pattern ${\bf x}$ to the input layer and generate the output ${\bf y}'$ at the output layer, which is compared with the desired output ${\bf y}$ to find the error ${\bf e}={\bf y}-{\bf y}'$;
  • Propagate the error backwards from the output layer to input layer to modify the weights so that the error, as a function of the weights, can be minimized.
  The weights are updated iteratively until eventually every input pattern presented to the input layer will cause the correct response pattern to appear at the output layer.

• Classification The network responds to various input patterns by generating the patterns associated to the input.

The forward pass is composed of two levels of computation: from the input to hidden:

$$z_{pj}=g(net^h_{pj})=g\left(\sum_{k=1}^N w_{jk}^h x_{pk}+T^h_j\right),\;\;\;\;\;\;(j=1,\cdots,L)$$

and from hidden to output:

$$y_{pi}=g(net^o_{pi})=g\left(\sum_{j=1}^L w_{ij}^o z_{pj}+T^o_i\right) \;\;\;\;\;\;(i=1,\cdots,M)$$

Here $p$ is the index for the $K$ pairs of patterns $\{({\bf x}_p, {\bf y}_p), p=1,2,\cdots,K\}$, and $w_{ij}^o$ and $w_{jk}^h$ are the weights of the hidden and output layers, respectively. $T^h_j$ and $T^o_i$'s are some threshold values associated with the jth hidden node and ith output node, respectively. For simplicity, we will drop the subscript $p$ in the following.

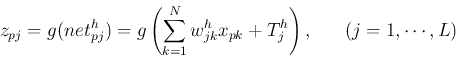
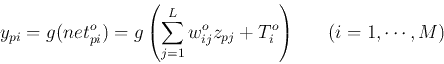
The calculation above can also be expressed in matrix form:

$${\bf z}_{L\times 1}=g\left({\bf W}^h_{L\times N} {\bf x}_{N\times 1}+{\bf T}^h_{L\times 1}\right)$$

and

$${\bf y}'_{M\times 1}=g\left({\bf W}^o_{M\times L} {\bf z}_{L\times 1}+{\bf T}^o_{M\times 1}\right)$$

For example, in supervised classification, the number of output nodes $M$ can be set to be the same as the number of classes $C$, i.e., $M=C$, and the desired output for an input ${\bf x}$ belonging to class $c$ is ${\bf y}=[0,\cdots,0,1,0,\cdots,0]^T$, for all output nodes to output 0 except the c-th one which should output 1 (one-hot method).