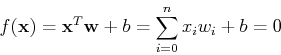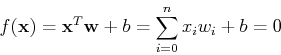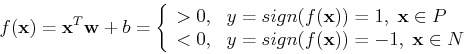Next: The learning problem:
Up: Support Vector Machines (SVM)
Previous: Support Vector Machines (SVM)
This is a variation of the perceptron learning algorithm.
Consider a hyper plane in an n-dimensional (n-D) feature space:
where the weight vector 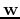 is normal to the plane, and
is normal to the plane, and 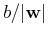 is the distance from the origin to the plane. The n-D space is partitioned
by the plane into two regions. We further define a mapping function
is the distance from the origin to the plane. The n-D space is partitioned
by the plane into two regions. We further define a mapping function
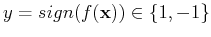 , i.e.,
, i.e.,
Any point 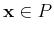 on the positive side of the plane is mapped to 1,
while any point
on the positive side of the plane is mapped to 1,
while any point 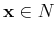 on the negative side is mapped to -1. A point
on the negative side is mapped to -1. A point
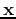 of unknown class will be classified to P if
of unknown class will be classified to P if 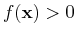 , or N
if
, or N
if 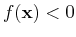 .
.
Ruye Wang
2015-08-13