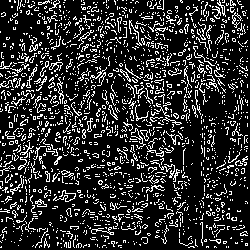Next: Difference of Gaussian (DoG)
Up: gradient
Previous: The Laplace Operator
As Laplace operator may detect edges as well as noise (isolated, out-of-range),
it may be desirable to smooth the image first by a convolution with a Gaussian
kernel of width 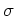
to suppress the noise before using Laplace for edge detection:
The first equal sign is due to the fact that
So we can obtain the Laplacian of Gaussian
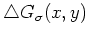 first and then convolve it with the input image. To do so, first consider
first and then convolve it with the input image. To do so, first consider
and
Note that for simplicity we omitted the normalizing coefficient
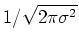 . Similarly we can get
. Similarly we can get
Now we have LoG as an operator or convolution kernel defined as
The Gaussian 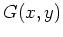 and its first and second derivatives
and its first and second derivatives 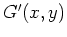 and
and
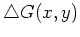 are shown here:
are shown here:
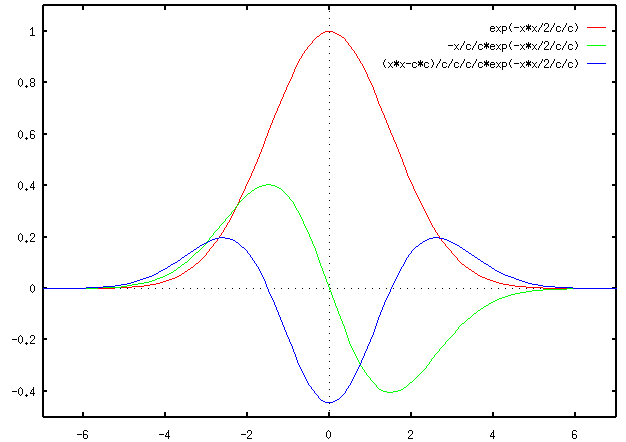
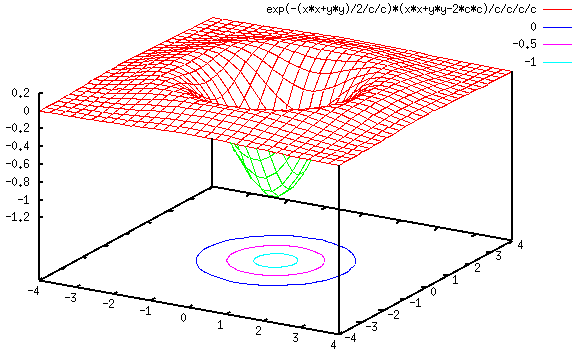
This 2-D LoG can be approximated by a 5 by 5 convolution kernel such as
The kernel of any other sizes can be obtained by approximating the
continuous expression of LoG given above. However, make sure that the
sum (or average) of all elements of the kernel has to be zero (similar
to the Laplace kernel) so that the convolution result of a homogeneous
regions is always zero.
The edges in the image can be obtained by these steps:
- Applying LoG to the image
- Detection of zero-crossings in the image
- Threshold the zero-crossings to keep only those strong ones
(large difference between the positive maximum and the negative minimum)
The last step is needed to suppress the weak zero-crossings most likely
caused by noise.



Next: Difference of Gaussian (DoG)
Up: gradient
Previous: The Laplace Operator
Ruye Wang
2016-10-18
![]()
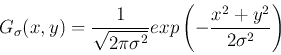
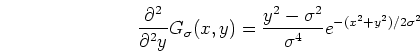
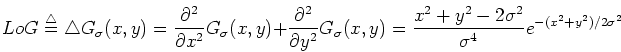
![]() and its first and second derivatives
and its first and second derivatives ![]() and
and
![]() are shown here:
are shown here:


![\begin{displaymath}
\left[ \begin{array}{ccccc}
0 & 0 & 1 & 0 & 0 \\
0 & 1 &...
...
0 & 1 & 2 & 1 & 0 \\
0 & 0 & 1 & 0 & 0 \end{array} \right]
\end{displaymath}](img105.png)