Edge Detection

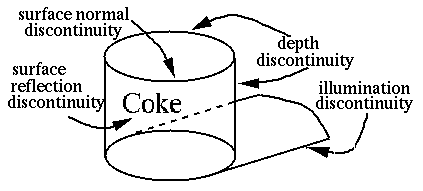
In most applications edges and lines in images carry more useful information than other types of features such as texture, color, etc. Edges and lines may be caused by various reasons:

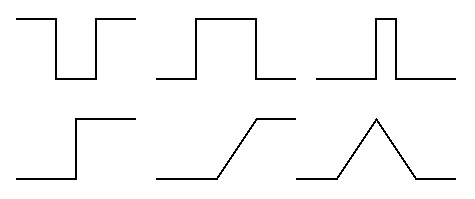
Edge detection is one of the most essential tasks in image processing. As edges and lines are drastic changes in gray level over a small spatial distance, they correspond to high spatial frequency components in the image signal. The main challenge is to distinguish edges from other small features in the image such as textures and especially the noise, so that all edges are detected while the noise is suppressed.

The gradient operator is sensitive to local gray level changes and is therefore a convenient tool to detect edges. If the magnitude $\vert g[m,n]\vert$ of the gradient image is larger than a threshold value, the pixel $[m,n]$ can be considered as on an edge. Moreover, the orientation of the edge can be obtained from the direction $\angle g[m,n]$ of the gradient vector. Some simple examples of 1-D case is shown below:

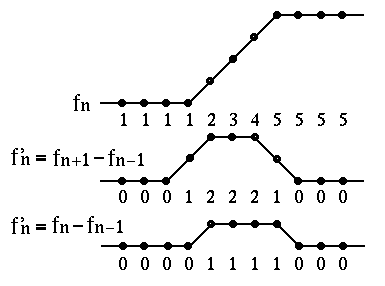
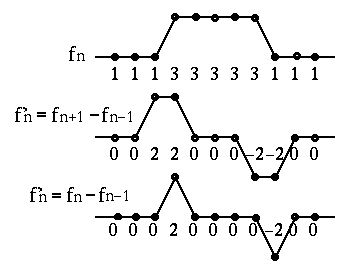
Edge detection by gradient operators (Roberts, Sobel and Prewitt):

However, when these gradient operators are used as edge detectors, their performances are very poor. Basically, they can not distinguish edges from textures and/or noise. The Prewitt gradient filter (3 by 3 and 5 by 5) is used to obtain the edges in the following image containing fuzzy edges:

Human vision is very good at edge detection. You can easily detect the edges in this image. But it may be very challenging to detect these edges by a computer. The difficulty of edge detection can be best appreciated by looking at the profile of the image shown on the top part of the image.