High-boost filtering

It is often desirable to emphasize high frequency components representing the image details (by means such as sharpening) without eliminating low frequency components representing the basic form of the signal. In this case, the high-boost filter can be used to enhance high frequency component while still keeping the low frequency components:

$$I_{hb}=I_o+c I_{hp}=(W_{ap}+c W_{hp})* I_o=W_{hb} * I_o$$

where c is a constant and $W_{hb}=c W_{ap}+W_{hp}$ is the high boost convolution kernel. For example:

• 
  
  $$W_{hb}=W_{ap}+c W_{hp} =\left[ \begin{array}{ccc} 0 & 0 ... ... -c & 0 -c & 4c+1 & -c \\ 0 & -c & 0 \end{array} \right]$$
  
  

• 
  
  $$W_{hb}=W_{ap}+c W_{hp} =\left[ \begin{array}{ccc} 0 & 0 & 0... ... & -c -c & 8c+1 & -c \\ -c & -c & -c \end{array} \right]$$
  
  

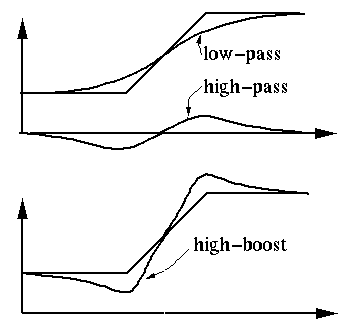
The example below shows the effect of high-boost filtering obtained by the above high-boost convolution kernel with $c=2$. The image on the left is the original image, the one in the middle is high-boost filtered. Note that the low spatial frequency components (global, large black background and bight areas) are suppressed while the high spatial frequency components (the texture of the fur and the whiskers) are enhanced. After a linear stretch, the image on the right is obtained.