Appendix B: Kernels and Mercer's Theorem

Generally speaking, a kernel is a continuous function $k(x,y)$ that takes two arguments $x$ and $y$ (real numbers, functions, vectors, etc.) and maps them to a real value independent of the order of the arguments, i.e., $k(x,y)=k(y,x) \in {\cal R}$.

Examples:

• ${\bf x}$ and ${\bf y}$ can be two n-dimensional vectors and
  
  $$k({\bf x},{\bf y})={\bf x}^T {\bf y}=\sum_n x_n y_n=k({\bf y},{\bf x})$$
  
  
  Or the kernel can be defined as
  
  $$k({\bf x},{\bf y})=exp(-\vert\vert{\bf x}-{\bf y}\vert\vert^2/2\sigma^2)$$
  
  

• $x(t)$ and $y(t)$ can be two functions and
  
  $$k(x(t),y(t))=\int x(t) y(t) dt=k(y(t),x(t))$$
  
  

• $x(t)$ and $y(t)$ can be two functions and their convolution is the kernel:
  
  $$k(x(t),y(t))=x(t)*y(t)=\int_{-\infty}^{\infty} x(\tau) y(t-\tau) d\tau =y(t)*x(t)=k(y(t),x(t))$$
  
  
  where $t$ is a parameter.

Mercer's theorem:

A kernel is a continuous function that takes two variables $x$ and $y$ and map them to a real value such that $k(x,y)=k(y,x)$.

A kernel is non-negative definite iff:

$$\int \int f(x) k(x,y) f(y) dx\;dy \ge 0$$

In association with a kernel $k$, we can define an integral operator $T_k$, which, when applied to a function $f(x)$, generates another function:

$$T_k( f(x) )=\int k(x,y)f(y)dy=[T_k\; f](x)$$

The eigenvalues and their correponding eigenfunctions of this operation are defined as:

$$T_k( \phi_i(x) )=\int k(x,y)\phi(y)dy=\lambda_i \phi_i(x)$$

The eigenvalues $\lambda_i$ are non-negative and the eigenfunctions $\phi_i(x)$ are orthonomal:

$$\int \phi_(x) \phi_j(x) dx=\delta_{ij}$$

The eigenfunctions corresponding to the non-zero eigenvalues form a set of basis functions so that the kernel can be decomposed in terms of them:

$$k(x,y)=\sum_{i=1}^\infty \lambda_i \phi_i(x) \phi_j(y)$$

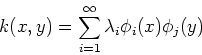
The above discussion can be related to a non-negative $N\times N$ matrix

$${\bf A}=\left[ \begin{array}{ccc} ...&...&...\\ ...&a[m,n]&...\\ ...&...&... \end{array} \right]_{N\times N}$$

A symmetric matrix ${\bf A}^T={\bf A}$ is positive definite iff

$$\sum_{m=1}^N \sum_{n=1}^N x[m] a[m,n] y[n] \ge 0, \;\;\;\mbox{or}\;\;\;\;{\bf x}^T {\bf A} {\bf y}\ge 0$$

where ${\bf x}=[x[1],\cdots,x[N]]^T$ and ${\bf y}=[y[1],\cdots,y[N]]^T$ are any two non-zero vectors.

A matrix defines a linear operation, which, when applied to a vector ${\bf x}$, generates another vector ${\bf y}$:

$$\sum_{m=1}^N a[m,n]x[m]=y[m],\;\;\;\;\mbox{or}\;\;\;\; {\bf A}{\bf x}={\bf y}$$

The eigenvalues and their correponding eigenfunctions of this operation are defined as:

$$\sum_{m=1}^N a[m,n] \phi_i[m] =\lambda_i \phi_i[n], \;\;\;\;\mbox{or}\;\;\;\; {\bf A} \phi_i=\lambda_i \phi_i$$

The eigenvalues $\lambda_i$ are non-negative and the eigenvectors $\phi_i$ are orthonomal:

$$\sum_{n=1}^N \phi_i[n] \phi_j[n] =\delta_{ij},\;\;\;\;\mbox{or}\;\;\; \phi_i^T \phi_j=\delta_{ij}$$

The eigenvectors corresponding to the non-zero eigenvalues form a set of basis vectors so that the matrix ${\bf A}$ can be decomposed in terms of them:

$$a[m,n]=\sum_{i=1}^N \lambda_i \phi_i[m] \phi_j[n]$$

i.e.

$${\bf A}\Phi =\Phi \Lambda,\;\;\;\;\mbox{or}\;\;\;\; {\bf A}=\Phi \Lambda \Phi^T$$

where $\Phi=[\phi_1,\cdots,\phi_N]$ and $\Lambda=diag[\lambda_1,\cdots,\lambda_N]$