Next: Marginal and conditional distributions
Up: Appendix A: Conditional and
Previous: Appendix A: Conditional and
Theorem 1
Proof:
Theorem 2 (inverse of a partitioned symmetric matrix)
Divide an 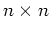 symmetric matrix
symmetric matrix 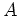 into four blocks
into four blocks
The inverse matrix 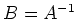 can also be divided into four blocks:
can also be divided into four blocks:
Here we assume the dimensionalities of these blocks are:
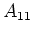 and
and 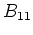 are
are 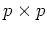 ,
,
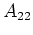 and
and 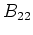 are
are 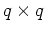 ,
,
-
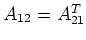 and
and
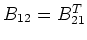 are
are 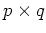
with 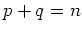 . Then we have
. Then we have
Proof:
i.e.,
Plug 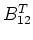 into
into 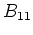 to get
to get
or
or
Applying theorem 1 to this expression, we also get the other expression in
the theorem. Similarly we can get
and
Theorem 3 (Determinant of a partitioned symmetric matrix)
Proof: Note that
The theorem is proved as we also know that
and



Next: Marginal and conditional distributions
Up: Appendix A: Conditional and
Previous: Appendix A: Conditional and
Ruye Wang
2006-11-14
![]() symmetric matrix
symmetric matrix ![]() into four blocks
into four blocks
![\begin{displaymath}A=\left[ \begin{array}{cc} A_{11} & A_{12} A_{21} & A_{22}...
...cc} A_{11} & A_{12} A_{12}^T & A_{22}
\end{array} \right]
\end{displaymath}](img130.png)
![\begin{displaymath}B=A^{-1}=\left[ \begin{array}{cc} B_{11} & B_{12} B_{21} &...
...cc} B_{11} & B_{12} B_{12}^T & B_{22}
\end{array} \right]
\end{displaymath}](img132.png)
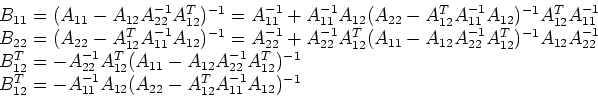
![$\displaystyle AA^{-1}=AB=\left[\begin{array}{cc}A_{11}&A_{12} A_{12}^T&A_{22...
...ight]
\left[\begin{array}{cc}B_{11}&B_{12} B_{12}^T&B_{22}\end{array}\right]$](img145.png)
![$\displaystyle \left[\begin{array}{cc}A_{11}B_{11}+A_{12}B_{12}^T&A_{11}B_{12}+A...
...22} \end{array}\right]
=\left[\begin{array}{cc}I_p&0 0&I_q\end{array}\right]$](img146.png)
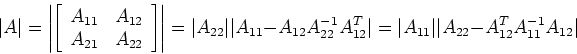
![$\displaystyle A=\left[\begin{array}{cc}A_{11}&A_{12} A_{21}&A_{22}\end{array} \right]$](img159.png)
![$\displaystyle \left[\begin{array}{cc}A_{11}&0 A_{12}^T&I \end{array}\right]
...
...c}I&A_{11}^{-1}A_{12} 0&A_{22}-A_{12}^TA_{11}^{-1}A_{12}
\end{array} \right]$](img160.png)
![$\displaystyle \left[\begin{array}{cc}I&A_{12} 0&A_{22} \end{array}\right]
\l...
...cc}A_{11}-A_{12}A_{22}^{-1}A_{12}^T&0\\
A_{22}^{-1}A_{21}&I\end{array} \right]$](img161.png)