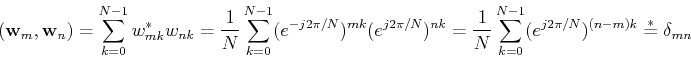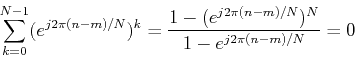Next: An Example
Up: fourier
Previous: The function and orthogonal
The summation expression for DFT
can also be written more conveniently as a matrix-vector multiplication:
and
It is obvious that the complexity of 1D DFT takes is 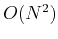 , which, as we
will see later, can be reduced to
, which, as we
will see later, can be reduced to
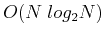 by Fast Fourier Transform
(FFT) algorithms.
by Fast Fourier Transform
(FFT) algorithms.
These matrix-vector multiplications can be represented more concisely as:
and
where both 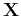 and
and 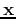 are
are 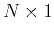 column (vertical) vectors:
column (vertical) vectors:
and 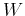 is an
is an 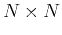 matrix:
matrix:
where 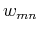 is an element in the mth row and nth column of matrix
is an element in the mth row and nth column of matrix 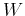 and
and 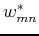 is its complex conjugate:
is its complex conjugate:
Obviously 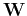 is symmetric (
is symmetric (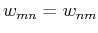 )
)
but 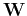 is not Hermitian:
is not Hermitian:
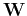 is a unitary matrix,
is a unitary matrix,
because its rows (or columns) are orthogonal:
This is because:
The DFT pair can be rewritten as:
See additional geometric explanation
of unitary/orthogonal transform.



Next: An Example
Up: fourier
Previous: The function and orthogonal
Ruye Wang
2009-12-31
![\begin{displaymath}X[n]=\frac{1}{\sqrt{N}}\sum_{m=0}^{N-1} x[m]e^{-mn j2\pi/N}
...
...0}^{N-1} X[n]e^{mn j2\pi/N}
=\sum_{n=0}^{N-1} w_N^{-mn} X[n] \end{displaymath}](img32.png)
![\begin{displaymath}X[n]=\frac{1}{\sqrt{N}}\sum_{m=0}^{N-1} x[m]e^{-mn j2\pi/N}
...
...0}^{N-1} X[n]e^{mn j2\pi/N}
=\sum_{n=0}^{N-1} w_N^{-mn} X[n] \end{displaymath}](img32.png)
![\begin{displaymath}\left[ \begin{array}{c} X[0] . . X[N-1] \end{array} \r...
...t[ \begin{array}{c} x[0] . . x[N-1] \end{array} \right]
\end{displaymath}](img72.png)
![\begin{displaymath}\left[ \begin{array}{c} x[0] . . x[N-1] \end{array} \r...
...t[ \begin{array}{c} X[0] . . X[N-1] \end{array} \right]
\end{displaymath}](img73.png)
![\begin{displaymath}{\bf X}\stackrel{\triangle}{=}
\left[ \begin{array}{c} X[0] ...
...y}{c} x[0] . . x[N-1] \end{array}
\right]_{N\times 1}
\end{displaymath}](img81.png)
![\begin{displaymath}{\bf W}=\left[ \begin{array}{ccc} . & . & . . & w_{mn} & . \\
. & . & . \end{array} \right]_{N\times N}
\end{displaymath}](img84.png)