


Next: The function and orthogonal
Up: fourier
Previous: Heisenberg Uncertainty Principle
Here we only consider the FT of continuous and periodic signals. The result
here should be easily generalized to other cases. The Fourier expansion of a
1D periodic signal
represents the signal as a weighted sum of complex exponential functions.
Here ![$X[n]$](img19.png) is the weight of the nth term (the Fourier coefficient) which
is in general a complex number
is the weight of the nth term (the Fourier coefficient) which
is in general a complex number
where
We assume the signal
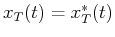 is real, then
is real, then ![$X[-n]=X^*[n]$](img56.png) , and we can
rewrite the Fourier expansion of
, and we can
rewrite the Fourier expansion of  above as
above as
where
![$ X[0]=\frac{1}{T}\int_T x(t) dt $](img62.png) is the average or DC component of the signal.
Now we see that any real signal
is the average or DC component of the signal.
Now we see that any real signal  can be represented as a weighted sum of infinite
number of sinusoids of different frequencies
can be represented as a weighted sum of infinite
number of sinusoids of different frequencies 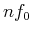 with different amplitudes
with different amplitudes ![$2X[n]$](img64.png) and
phases
and
phases ![$\angle X[n]$](img65.png) .
.



Next: The function and orthogonal
Up: fourier
Previous: Heisenberg Uncertainty Principle
Ruye Wang
2009-12-31
![\begin{displaymath}x_T(t)=\sum_{n=-\infty}^{\infty} X[n]e^{j2\pi nf_0t} \end{displaymath}](img52.png)
![\begin{displaymath}x_T(t)=\sum_{n=-\infty}^{\infty} X[n]e^{j2\pi nf_0t} \end{displaymath}](img52.png)
![\begin{displaymath}\left\{ \begin{array}{l}
\vert X[n]\vert=\sqrt{X_r[n]^2+X_j[...
...
\angle{X[n]}=tan^{-1} [ X_j[n]/X_r[n] ] \end{array} \right.
\end{displaymath}](img54.png)
![$\displaystyle \sum_{n=-\infty}^{\infty} X[n]e^{j2\pi nf_0t}
= X[0]+\sum_{n=1}^{\infty}[ X[n]e^{j2\pi nf_0t}+X[-n]e^{-j2\pi nf_0t}]$](img59.png)
![$\displaystyle X[0]+\sum_{n=1}^{\infty}[ X[n]e^{j2\pi nf_0t}+X^*[n]e^{-j2\pi nf_...
...j\angle X[n]}e^{j2\pi nf_0t}+\vert X[n]\vert e^{-j\angle X[n]}e^{-j2\pi nf_0t}]$](img60.png)
![$\displaystyle X[0]+\sum_{n=1}^{\infty} \vert X[n]\vert [e^{j(2\pi nf_0+\angle X...
...] )}]
= X[0]+\sum_{n=1}^{\infty} 2\vert X[n]\vert\;cos(2\pi nf_0t+\angle X[n] )$](img61.png)