


Next: Fast DCT algorithm
Up: dct
Previous: dct
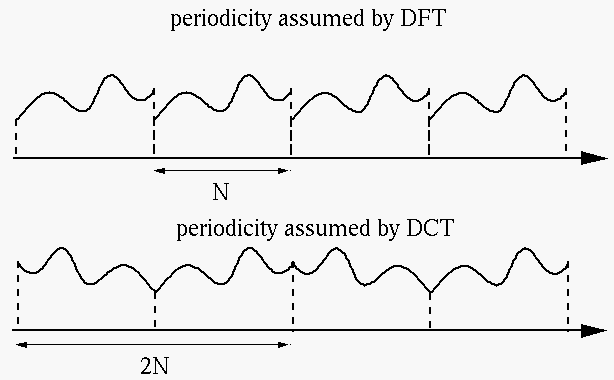
The discrete Fourier transform (DFT) transforms a complex signal into its
complex spectrum. However, if the signal is real as in most of the applications,
half of the data is redundant. In time domain, the imaginary part of the signal
is all zero; in frequency domain, the real part of the spectrum is even symmetric
and imaginary part odd. In comparison, Discrete cosine transform (DCT) transforms
is a real transform that transforms a sequence of real data points into its real
spectrum and therefore avoids the problem of redundancy. Also, as DCT is derived
from DFT, all the desirable properties of DFT (such as fast algorithm) are preserved.
To derive the DCT of an N-point real signal sequence
![$\{x[m],\;\;\;(m=0,\cdots,N-1)\;\}$](img1.png) , we first construct a new sequence of
, we first construct a new sequence of 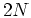 points:
points:
This 2N-point sequence ![$x'[m]$](img4.png) is assumed to repeat its self outside the range
is assumed to repeat its self outside the range
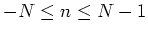 , i.e., it is periodic with period
, i.e., it is periodic with period 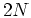 , and it is even
symmetric with respect to the point
, and it is even
symmetric with respect to the point 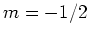 :
:
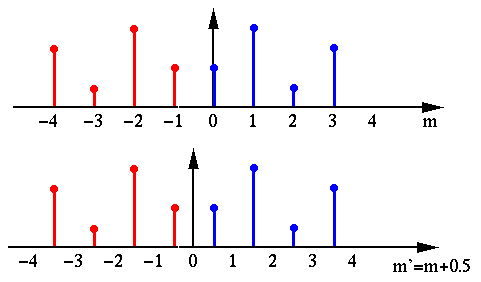
If we shift the signals ![$x'[m]$](img4.png) to the right by 1/2, or, equivalently, shift
to the right by 1/2, or, equivalently, shift
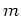 to the left by 1/2 by defining another index
to the left by 1/2 by defining another index 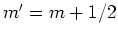 , then
, then
![$x'[m]=x'[m'-1/2]$](img10.png) is even symmetric with respect to
is even symmetric with respect to 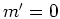 .
In the following we simply represent this new function by
.
In the following we simply represent this new function by ![$x[m]$](img12.png) .
.
The DFT of this 2N-point even symmetric sequence can be found as:
Note that the second summation above is zero. This is because ![$x[m]$](img12.png) is even and
is even and
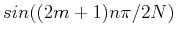 is odd with respect to
is odd with respect to 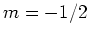 , all terms in the second
summation are odd and the summation is zero (while all terms in the first summation
are even). It can also be seen that all
, all terms in the second
summation are odd and the summation is zero (while all terms in the first summation
are even). It can also be seen that all ![$X[n]$](img19.png) is real and even
is real and even ![$X[n]=X[-n]$](img20.png) . Next,
we replacie
. Next,
we replacie 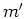 by
by 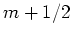 and get
and get
Note that since all terms in the summation are even, only the first half of the
data points need to be used. Moreover, as cosine function is even, ![$X[n]=X[-n]$](img20.png) is also even and periodic with period
is also even and periodic with period 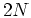 , we have
, we have
![$X[N+n]=X[N+n-2N]=X[-N+n]=X[N-n]$](img25.png) ,
indicating that a point
,
indicating that a point ![$X[N+n]$](img26.png) (
(
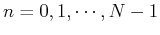 ) in the second half is the
same as its corresponding point
) in the second half is the
same as its corresponding point ![$X[N-n]$](img28.png) in the first half, i.e., the second half
is redundant and therefore can be dropped. Now we have the discrete cosine transform
(DCT):
in the first half, i.e., the second half
is redundant and therefore can be dropped. Now we have the discrete cosine transform
(DCT):
where ![$c[n,m]$](img30.png) the nth row and mth column of the DCT matrix:
the nth row and mth column of the DCT matrix:
All row vectors of this DCT matrix are orthogonal and normalized except the first
one (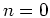 ):
):
To make DCT a orthonormal transform, we define a coefficient
so that DCT now becomes
where ![$c[n,m]$](img30.png) is modified with
is modified with ![$a[n]$](img36.png) , which is also the component in the nth
row and mth coloum of the N by N cosine transform matrix:
, which is also the component in the nth
row and mth coloum of the N by N cosine transform matrix:
Here
![${\bf c}_i^T=[c[i,0],\cdots,c[i,N-1]$](img38.png) is the ith row of the DCT transform
matrix
is the ith row of the DCT transform
matrix 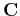 . As these row vectors are orthogonal:
. As these row vectors are orthogonal:
the DCT matrix 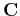 is orthogonal:
is orthogonal:
and it is real
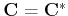 . Now the DCT can be expressed in matrix form as:
. Now the DCT can be expressed in matrix form as:
The inverse DCT is
or in matrix form:
Example: A 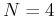 -point DCT matrix can be generated by
-point DCT matrix can be generated by
![$c[n,m]=a[n] cos( (2m+1)n\pi/8)$](img47.png) to be
to be
Assume the signal is
![${\bf x}=[0\; 1\; 2\; 3]^T$](img49.png) , then its DCT transform is:
, then its DCT transform is:
The inverse transform is:
This result is very similar to the example shown in the previous section for
WHT transform. In fact, these two transforms are very comparible, as seen from
the figure below:
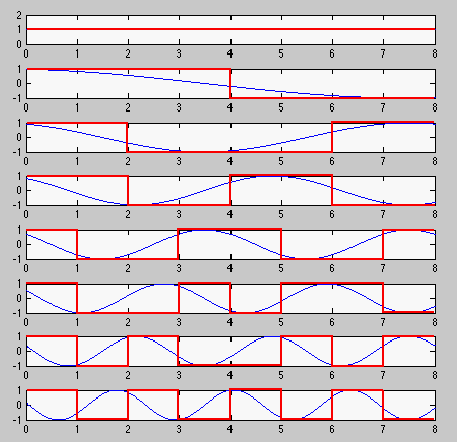
Compared with DFT, DCT has two main advantages:
- It is a real transform with better computational efficiency than DFT
which by definition is a complex transform.
- It does not introduce discontinuity while imposing periodicity in the
time signal. In DFT, as the time signal is truncated and assumed periodic,
discontinuity is introduced in time domain and some corresponding artifacts
is introduced in frequency domain. But as even symmetry is assumed while
truncating the time signal, no discontinuity and related artifacts are
introduced in DCT.



Next: Fast DCT algorithm
Up: dct
Previous: dct
Ruye Wang
2009-10-13
![]() , we first construct a new sequence of
, we first construct a new sequence of ![]() points:
points:
![\begin{displaymath}x'[m]\stackrel{\triangle}{=}\left\{ \begin{array}{ll}
x[m] ...
...\leq N-1) x[-m-1] & (-N \leq m \leq -1)
\end{array} \right. \end{displaymath}](img3.png)

![$\displaystyle \frac{1}{\sqrt{2N}} \sum_{m'=-N+1/2}^{N-1/2} x[m'-\frac{1}{2}]e^{-j2\pi m'n/2N}$](img15.png)
![$\displaystyle \frac{1}{\sqrt{2N}} \sum_{m=-N+1/2}^{N-1/2}x[m'-\frac{1}{2}]\;cos...
...ac{j}{\sqrt{2N}} \sum_{m=-N}^{N-1/2}x[m'-\frac{1}{2}]\;sin(\frac{2\pi m'n}{2N})$](img16.png)
![$\displaystyle \frac{1}{\sqrt{2N}} \sum_{m=-N+1/2}^{N-1/2}x[m'-\frac{1}{2}]\;cos(\frac{2\pi m'n}{2N})
\;\;\;\;\;\;\;(n=0,\cdots,2N-1)$](img17.png)
![$\displaystyle \frac{1}{\sqrt{2N}} \sum_{m=-N+1/2}^{N-1/2}x[m'-\frac{1}{2}]\;cos...
...'n}{2N})
=\frac{1}{\sqrt{2N}} \sum_{m=-N}^{N-1}x[m]\;cos(\frac{(2m+1)n\pi}{2N})$](img23.png)
![$\displaystyle \sqrt{\frac{2}{N}} \sum_{m=0}^{N-1}x[m]\;cos(\frac{(2m+1)n\pi}{2N}),
\;\;\;\;\;\;\;(n=0,\cdots,2N-1)$](img24.png)
![\begin{displaymath}X[n]=\sqrt{\frac{2}{N}} \sum_{m=0}^{N-1}x[m]\;cos(\frac{(2m+1...
...
=\sum_{m=0}^{N-1} c[n,m]x[m], \;\;\;\;\;\;\;(n=0,\cdots,N-1) \end{displaymath}](img29.png)
![\begin{displaymath}c[n,m]\stackrel{\triangle}{=}\sqrt{\frac{2}{N}}cos(\frac{ (2m+1)n\pi}{2N})
\;\;\;\;\;(m,n=0,1,\cdots,N-1) \end{displaymath}](img31.png)
![\begin{displaymath}\sqrt{\sum_{m=0}^{N-1}c^2[n,m]}=
\sqrt{\sum_{m=0}^{N-1}\;\fra...
...sqrt{2} & (n=0) 1 & (n=1,2,\cdots,N-1)
\end{array} \right. \end{displaymath}](img33.png)
![\begin{displaymath}a[n]=\left\{ \begin{array}{ll} \sqrt{1/N} & \mbox{for $n=0$} ...
...rt{2/N} &
\mbox{for $ n=1,2,\cdots,N-1$} \end{array} \right.
\end{displaymath}](img34.png)
![\begin{displaymath}X[n] = a[n] \sum_{m=0}^{N-1}x[m]\;cos(\frac{ (2m+1)n\pi}{2N})
=\sum_{m=0}^{N-1}x[m]\;c[n,m]\;\;\;\;\;\;\;(n=0,\cdots,N-1)
\end{displaymath}](img35.png)
![\begin{displaymath}\left[ \begin{array}{ccc} \cdots & \cdots & \cdots \\
\cdots...
...^T \cdots {\bf c}_{N-1}^T \end{array} \right]
={\bf C}^T \end{displaymath}](img37.png)
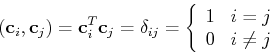
![\begin{displaymath}x[m] = \sum_{n=0}^{N-1} X[n]\;c[m,n]=
\sum_{n=0}^{N-1} a[n] X...
...})
=\sum_{n=0}^{N-1}X[n]\;c[n,m]\;\;\;\;\;\;\;(m=0,\cdots,N-1) \end{displaymath}](img44.png)
![]() -point DCT matrix can be generated by
-point DCT matrix can be generated by
![]() to be
to be
![\begin{displaymath}{\bf C}^T=\left[ \begin{array}{c} {\bf c}_0^T \\ \vdots \\ {\...
....50 & 0.50 \\
0.27 & -0.65 & 0.65 & -0.27 \end{array} \right] \end{displaymath}](img48.png)
![\begin{displaymath}{\bf X}={\bf C}^T {\bf x}=\left[ \begin{array}{rrrr}
0.50 & ...
...egin{array}{r} 3.00 -2.23 0.00 -0.16 \end{array} \right] \end{displaymath}](img50.png)
![\begin{displaymath}{\bf x}={\bf C} {\bf X}=\left[ \begin{array}{rrrr}
0.50 & 0....
...ht]
=\left[ \begin{array}{r} 0 1 2 3 \end{array} \right] \end{displaymath}](img51.png)

