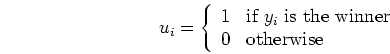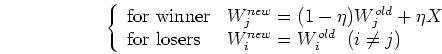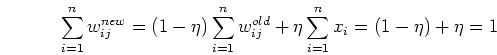Next: About this document ...
Up: bp
Previous: The Structure and Purpose
For mathematical convenience, we assume
- All patterns are binary:
- All weights of an output node
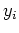 are normalized:
are normalized:
During training, all input patterns are presented to the input layer one at a
time in a random order. Every time a pattern 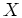 is presented to the input
layer of the network, the weights are modified by the following learning law:
is presented to the input
layer of the network, the weights are modified by the following learning law:
where
and 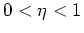 is the learning rate.
is the learning rate.
This learning law can now be written as
We note that the new weight vector is still normalized:
We see that the winner's weight vector is modified so that it moves closer
towards the current input vector 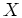 while all other weights are unchanged.
Since for an output node
while all other weights are unchanged.
Since for an output node 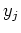 to win, its weight vector
to win, its weight vector 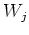 has to satisfy
has to satisfy
where 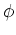 is the angle between the two vectors
is the angle between the two vectors 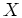 and
and 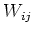 , in other
words, the distance between
, in other
words, the distance between 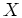 and
and 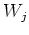
must be smaller than that between 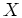 and any other
and any other 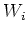 , we realize that
the learning law will always pulls the weight vector closest to the current
input vector even closer towards the input vector, so that the corresponding
winning node will be more likely to win whenever a pattern similar to the
current
, we realize that
the learning law will always pulls the weight vector closest to the current
input vector even closer towards the input vector, so that the corresponding
winning node will be more likely to win whenever a pattern similar to the
current 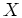 is presented in the future. The overall effect of such a learning
process is to pull the weight vector of each output node towards the center of
a cluster of similar input patterns and the corresponding node will always win
the competition whenever a pattern in the cluster is presented. If there exist
c clusters in the feature space, they will each be represented by an output
node. The remaining
is presented in the future. The overall effect of such a learning
process is to pull the weight vector of each output node towards the center of
a cluster of similar input patterns and the corresponding node will always win
the competition whenever a pattern in the cluster is presented. If there exist
c clusters in the feature space, they will each be represented by an output
node. The remaining 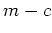 output nodes may never win and therefore do not
represent any cluster.
output nodes may never win and therefore do not
represent any cluster.



Next: About this document ...
Up: bp
Previous: The Structure and Purpose
Ruye Wang
2002-12-09
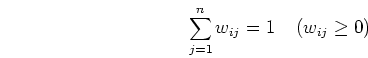
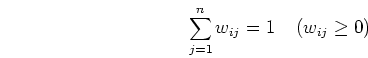
![]() is presented to the input
layer of the network, the weights are modified by the following learning law:
is presented to the input
layer of the network, the weights are modified by the following learning law: