The Gradient Descent Method

Given a 2-D function $f(x,y)$, the gradient descent method finds $(x_0, y_0)$ so that $f(x_0,y_0) \rightarrow \;min$.

First consider 1D case. We see that $x^{new}$ is always in the opposite direction of the increasing direction of $f(x)$:

$$x^{new}=x^{old}-\eta\;\frac{df}{dx}$$

where $\eta$ is the step size, or the learning rate in network training.

Then consider 2D case where the derivative used in 1D case becomes gradient

$${\bf G}=\bigtriangledown f(x,y)\stackrel{\triangle}{=} \frac{... ...\frac{\partial f}{\partial y} {\bf j} =f_x {\bf i}+f_y {\bf j}$$

Or, in vector form,

$$G=[f_x, f_y]^T$$

Now gradient descent becomes

$$X^{new}=X^{old}-\eta\;G$$

i.e.,

$$\left\{ \begin{array}{l} x^{new}=x^{old}-\eta\,f_x \\ y^{new}=y^{old}-\eta\,f_y \end{array} \right.$$

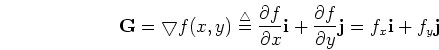
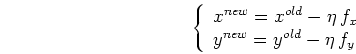
Obviously the gradient descent method can be generalized to minimize high dimensional functions $f(x_1,\cdots,x_n)$.