"Both Werckmeister and Neidhardt had a proper respect for equal temperament also, but a fanatic like Tempelhof, writing fifty to seventy-five years later, could say that equal temperament was the worst possible temperament because one scale must differ from another in its tuning!"
-- J. Murray Barbour: Tuning and Temperament: A Historical Survey, (East Lansing: Michigan State College Press, 1953), p. 157.
Even before I had thought of using just tuning systems in my own composition, I knew that Barbour was something of a fanatic himself. My own interest in and study of early music had taught me that composers from the baroque period knew about equal temperament but made a conscious decision to avoid it. Obviously, it was more important for some to have better sounding thirds than to be able to play in A# minor, for example. However, some writers of the period preferred unequal tuning systems for another reason which was more interesting to me as a composer: maintaining distinct key characteristics.
Many theoretical works of the eighteenth century explicitly assign certain affectations or emotional characteristics to different keys. Though these writings often contradict each other as to what these characteristics actually are, it is well known that many composers carefully chose keys for similar affectations throughout their lives. To Mattheson, for example, D major was "somewhat shrill and stubborn," while to Rousseau it was suited to "gaiety or brilliance."
People with perfect pitch and absolute pitch memory will certainly be able to remember certain associations, but what of the rest of us? If one had enough "proper respect" for equal temperament to tune one's harpsichord that way, why should emotional affectation matter at all in the composer's choice of key?
Of course the choice matters because composers of that period did not use equal temperament and the keys did sound distinctly different. In fact, the poor fanatic Georg Friedrich Tempelhof held a view quite common in the eighteenth century: that keys had different associative characteristics because of unequal temperament, and that if one adopted equal temperament, those characteristics would disappear.
Musicians who valued these characteristics and spoke out against equal temperament included Johann Mattheson, Jean-Jacques Rousseau, and Johann Philipp Kirnberger. [1] Kirnberger was even able to add the name of the great Johann Sebastian Bach to his cause through a testimonial by his son Emanuel, which contradicts the myth that the great Bach advocated equal temperament. Kirnberger went so far as to publish a table showing the ratios for his tuning system in every key, so that a composer could judge how "pure" a key would sound by the relative number of small-numbered ratios relative to that tonic.
The characterizations of keys began to matter to me as a composer when I began to experiment with just tuning systems and how they affected the process of composition. I was not as concerned with "traditional" harmonic progressions as some composers who use just intonation. Instead, I became interested in pitch sets which are used freely within a given section. This technique can be found in the music of the Indonesian gamelan and the compositions of Lou Harrison, and it has recently become a prominent idiom in the music of such composers as Steve Reich, Terry Riley, and John Adams.
In explaining his own evolution of style, John Adams credited his work with highly resonant filters in electronic music for his "rediscovery of the power of the harmonic series." This led to the composition of China Gates for piano (1976), Phrygian Gates for piano (1977), and Shaker Loops for string septet (1978). In each of these works, Adams typically builds up a diatonic pitch set over a period of time, adding new tones until all are present. Adams calls these sections "gates," borrowing the term from an analogous function in electronic music, and moments of great drama occur in the sudden transitions.
One might look at a gate as one enormously long eleventh (or whatever) chord and the harmonic rhythm as glacially slow, but I think such an analysis would be missing the point. The interest really lies in the constant and subtle shifting of the relationships of these tones within the patterns. A colleague of mine once criticized this technique as "anything-goes" harmony; that is, as long as one sticks to the pitch set there are no "wrong notes." I think he experienced the inevitable disappointment of one who looks for traditional counterpoint and harmonic progressions in such a piece.
Just relationships over a constant fundamental are more explicit in the works of Terry Riley and LaMonte Young. Adams has cited Riley's In C (1964), in fact, as one of the influences on Shaker Loops. Though the two composers' approach to composition is quite different, the use of constant pitch sets within a section are similar. In the 1960's Riley had his electronic organ tuned to just intonation and most often improvised on the harmonic series of an explicit or implied fundamental. This practice is related to improvisation above the drone in Indian music, a major influence on Riley.
Though I write sections with freely used pitch sets in my own composition, these sections have significant differences between those of Adams or Riley. Unlike Adams, they are frequently non-diatonic; instead, the "closeness" of the relationships of the tones in the pitch set to a fundamental determines the relative stability of the section, as well as its character. Unlike Riley, the sections and the transitions between them have carefully planned structural functions. The transitions may be gradual, pitches changing a semitone at a time, or sudden and dramatic.
Beginning in 1985, I had the opportunity to use a Synclavier II at the University of Southern California to realize electronic compositions. [2] While this instrument is very powerful, the tuning capability is limited to 12 pitches per octave (or a variable number of pitches per octave if you want to use microtonal equal temperament). Given this restriction, what I decided to do was to identify a certain limited number of fundamentals that I wanted to use for structurally important key centers.
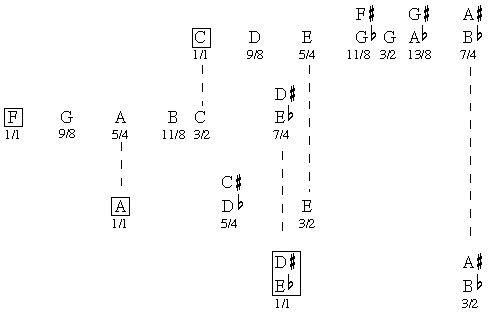
In Time Auscultations for example, I chose as primary fundamentals (tonal centers) C and F, with A and Eb being secondary fundamentals. The first thing I decided after choosing these key centers was that, to be stable at all, each of these tonal centers would have to have a 3/2 present above it. I chose the other available intervals based on which keys would have the most tonal stability, which intervals would be important melodically, how the transitions would occur, and other compositional criteria. The relative stability and character of each of these tonal centers, though, are defined by the ratios of the other pitches relative to them (see figure 1).

| C | C#/Db | D | D#/Eb | E | F | F#/Gb | G | G#/Ab | A | A#/Bb | B | C | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 25/24 | 9/8 | 7/6 | 5/4 | 4/3 | 11/8 | 3/2 | 13/8 | 5/3 | 7/4 | 11/6 | 2/1 |
| Frequency in hertz | 264 | 275 | 297 | 308 | 330 | 352 | 363 | 396 | 411 | 440 | 462 | 484 | 528 |
| Cents relative to C | 0 | 71 | 204 | 267 | 386 | 498 | 551 | 702 | 765 | 884 | 969 | 1049 | 1200 |
For example, with C as a fundamental, harmonics 9, 10 (5), 11, 12 (3), 13, and 14 (7) are available. In figure 1 these harmonics are represented by ratios within an octave, that is, each of the denominators is a power of two. The use of these pitches together within a pitch set results in a structurally and tonally very stable section within the piece. With A as a fundamental, harmonics 5 and 6 (3) are available, but the other intervals are not related by harmonic numbers relative to the A. They may still produce interesting and consonant intervals suitable for a structurally important section, but the relative stability will be far less than for a C fundamental. Figure 2 is a broad outline of the pitch sets used in Time Auscultations and their relationship to the formal structure.
Moreover, each of the sections will have a distinctive character. Melodic motives, for example, are repeated in the different pitch sets, but take on completely different characters as the pitches' relationships to the fundamental change. This change in character is similar to a theme being transposed from major to minor mode, but with far more gradations of mood. My experience with these tuning systems made me understand Mattheson's insistence that transposing a piece in an unequally-tempered system in effect put it in a different mode.
For example, figure 3 shows the central motive of Time Auscultations the first time it is heard. Four of the first five notes lie in the harmonic series above the implied C fundamental. The exception, Eb (6/5), is intentionally substituted for the 5th harmonic (E) throughout the following C fundamental section. The E natural is finally heard in the last section, which brings us back to the C fundamental, but with a different and more stable character, suitable to the ending (figure 4). This time all of the pitches in the pitch set are harmonically related to C with the exception of the A's, which occur because of the inversion of the principal motive.
This general procedure of determining a tuning system was used for my other justly-tuned electronic works. It is important to note that I have used a different tuning system for each piece, that is, I have not attempted to arrive at a single, all-encompassing, ur-scale. Instead, I have composed the tuning system as I would compose any other aspect of a piece. The ratios of the intervals depend on such factors as the melodies I want to use, the key centers I want to use, the characters I want the keys to have, and so on. Conversely, the melodies I compose are sometimes influenced by intervals I want to use. Of course, there's nothing wrong with sticking, like Partch, to a particular scale, and that approach is usually necessary if one builds one's own instruments. However, I have built my "instruments" in software.
In Instantaneous Motion I chose the primary fundamentals C, A, and Eb. As can be seen in figure 5, many of my favorite intervals carried over from Time Auscultations, but in this case I came up with another problem. I knew that both fundamentals A and C needed a 3/2 above them and I wanted G to be tuned a 7/4 above A because of the melodic importance of that interval. Finally, I knew I wanted a 5/4 E above C to have a strongly stable ending (as in Time Auscultations). As can be seen in figure 5, this sets up a conflict: 2 E's are needed. Not having split keys on the Synclavier, I had to record each of the sections with different E's on separate sequences and assemble them on the multitrack tape. Another wonderful melodic interval available in this tuning system is the 49/48 between C and C#. It is used prominently several times.
| C | C#/Db | D | D#/Eb | E | F | F#/Gb | G | G#/Ab | A | A#/Bb | B | C | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratios relative to C | 1/1 | 49/48 | 9/8 | 7/6 | 5/4 9/7 | 4/3 | 11/8 | 3/2 | 13/8 | 12/7 | 7/4 | 27/14 | 2/1 |
| Frequencies in hz | 257 | 262 | 289 | 299 | 321 330 | 342 | 353 | 385 | 417 | 440 | 449 | 495 | 513 |
| Intervals in cents | 0 | 36 | 204 | 267 | 386 435 | 498 | 551 | 702 | 840 | 933 | 969 | 1137 | 1200 |
The harmonic relationship of the pitch set to the fundamental is even more explicit in the beginning section of Bending Space. In the beginning, for example, a low C drone is heard for over a minute, but its third, seventh, and eleventh harmonics are resonated, that is, they get gradually louder and softer, becoming at times distinct pitches and at other times blending into the general timbre of the drone. Like Adams, I like highly resonant filters on analog synthesizers, and I was also influenced by the works by such composers as Jean-Claude Risset which play around the gray areas of timbral fusion.
While tuning systems and pitch sets are hardly the only factors which determine the character or mood of a section, they are very important in works in unequal tuning systems. I don't think I can verbally describe their effect, and, even if I could, they may have a quite different, and just as valid effect on someone else. However, like the composers of the eighteenth century, I feel that in equal temperament, this valuable dimension of music is lost.
[1] For a fairly comprehensive account of this controversy, see Steblin.
[2] The Synclavier II was purchased from a grant from the University of Southern California Faculty Research and Innovation Fund. With it I realized the six works on the Terrain of Possibilities CD (EMF 002). Time Auscultations is available on the Terrain of Possibilities cassette, as well as Rational Music for an Irrational World (Other Music, 1989). Both are available from the Just Intonation Network. The other works mentioned in this article are also available on the Terrain of Possibilities.
John Adams, Lecture at the University of Southern California, Nov. 1, 1985.
Johann Philipp Kirnberger, Die Kunst des reinen Satzes in der Musik, (Berlin and Königsberg: Decker & Hartung, 1774-79), facsimile repr. (Hildesheim: Georg Olms, 1968), vol. ii, p. 188. See also Steblin, p. 92.
Johann Mattheson, Das neueröffnete Orchestre (Hamburg, 1713), see translation in Steblin.
Johann Mattheson, Exemplarische Organisten-Probe, (Hamburg: Schiller, 1717): p. 66. See the translation in Steblin, p. 54.
Jean-Jacques Rousseau, "Ton" in Dictionnaire de musique (1768), see translation in Steblin, p. 64.
Updated on April 22, 1996 by Bill Alves (alves@hmc.edu).